Karel esta aprendiendo técnicas algorítmicas

Una de ellas se conoce como "Suma de prefijos", la cual es muy útil.

Karel recibe una lista de números de longitud \(N\) y él querrá obtener su Suma de prefijos.

Para entender que es la "Suma de prefijos" veamos un ejemplo en el que recibe una lista de longitud 4.

\[\{1, 2, 4, 7\}\]

Digamos que la lista se llama \(A\), y el primer elemento es \(A_1\), el segundo elemento es \(A_2\), el tercero \(A_3\) y el cuarto es \(A_4\).

De forma que, para la lista que vemos, los valores son:

• \(A_1 = 1\)
• \(A_2 = 2\)
• \(A_3 = 4\)
• \(A_4 = 7\)

La "Suma de prefijos" es una lista que se obtiene a partir de la lista original, es construida de forma de que el elemento número \(i\) es la suma de los primeros \(i\) números y tiene el mismo tamaño. Si llamamos a la Suma de prefijos como \(P\), entonces:

• El primer elemento de \(P\) es \(A_1\)
• El segundo elemento de \(P\) es \(A_1+A_2\)
• El tercer elemento de \(P\) es \(A_1+A_2+A_3\)
• El cuarto elemento de \(P\) es \(A_1+A_2+A_3+A_4\)

Es decir, para la lista

• \(P_1 = 1\)
• \(P_2 = 1+2 = 3\)
• \(P_2 = 1+2+4 = 7\)
• \(P_2 = 1+2+4+7 = 14\)

Problema

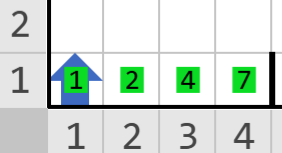
Karel recibe una lista de números \(A\) representada con zumbadores que inicia en \((1, 1)\) y continua horizontalmente hasta una pared delimitadora.

Cambia la lista de números por su suma de prefijos

Ejemplo 1

Mundo inicial

Mundo final

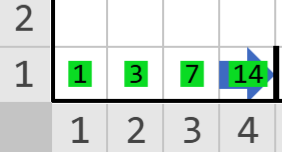
Este mundo es el del ejemplo que está arriba.

Ejemplo 2

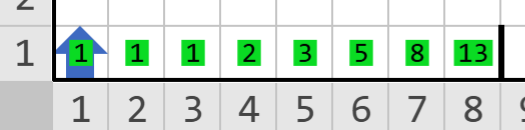
Mundo inicial

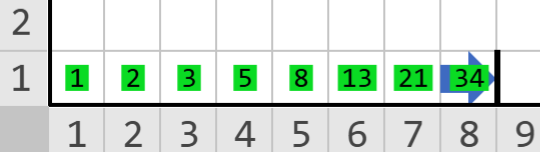
Salida

Consideraciones

• Karel inicia en \((1, 1)\) orientado al norte
• Karel tiene infinitos zumbadores en la mochila
• No importa la posición ni orientación final de Karel
• Debes dejar los zumbadores de la lista $P$ en el mismo lugar donde estaba la lista original.
• No debes dejar otros zumbadores en el mundo

Subtareas

• Para 30 puntos, la lista original esta llena solamente por \(1\)
• Para 70 puntos, no hay consideraciones extra