La muerte de Karel
Ver en PDFHistoria
Finalmente, Karel será castigado por sus crímenes contra la informática. Después de 13 años de hacer sufrir a los competidores de la OMI, el Comité de la Olimpiada Mexicana de Informática ha sentenciado a Karel a la muerte.
Sin embargo, antes de recibir su merecido, Karel tiene que esperar en una fila compuesta de varios prisioneros esperando su destino. Todos los prisioneros tienen alturas enteras y positivas.
La fila de los prisioneros está representada con montones de zumbadores en la primera fila; cada montón representa un prisionero y la cantidad de zumbadores en el montón representa su altura.
Todos los prisioneros están viendo a la izquierda. Cada prisionero puede ver sólo hasta el siguiente prisionero más alto hacia la izquierda o hasta la pared, ya que cualquiera de estas dos cosas le obstruyen su visión.
La fila de prisioneros está delimitada por paredes que hacen un mundo de una fila de alto y \(N\) columnas de ancho. En este mundo Karel se enfrenta con su último problema de la OMI:
Problema
Escribe un programa que, en cada posición de la primera fila del mundo, deje un montón de zumbadores igual a la altura del prisionero que obstruye la visión del prisionero que originalmente está en esa posición. En caso de que la visión del prisionero sea obstruida por la pared, deberás dejar 0 zumbadores en esa posición.
Consideraciones
- Karel inicia en la posición (1,1) y su orientación depende de la subtarea que se está ejecutando.
- Karel tiene infinitos zumbadores en su mochila.
- Cada posición en la fila tiene más de 0 y menos de 100 zumbadores.
- Para obtener puntos en este problema, Karel deberá dejar en cada posición de la primera fila un montón de zumbadores igual a la altura del prisionero que obstruye la visión del prisionero originalmente en esa posición. En caso de que el prisionero en esa posición alcance a ver hasta la pared, deberá dejar 0 zumbadores.
- No importan la orientación ni la posición final de Karel.
- No importa la cantidad final de zumbadores en la mochila de Karel.
- En este problema la cantidad máxima de instrucciones
avanza/moveque puede ejecutar Karel, así como las propiedades del mundo, cambian dependiendo de la subtarea.
Subtareas
Subtarea 1 [18 puntos]
- Karel empieza orientado al norte.
- Si hay \(N\) columnas en el mundo, Karel podrá ejecutar
avanza/move\(N\times(N+1)\) veces.
Subtarea 2 [24 puntos]
- Karel empieza orientado al sur.
- Todas las casillas tienen menos de 10 zumbadores.
- Si hay \(N\) columnas en el mundo, Karel podrá ejecutar
avanza/move\(20N\) veces.
Subtarea 3 [58 puntos]
- Karel empieza con una orientación desconocida.
- Si hay \(N\) columnas en el mundo, Karel podrá ejecutar
avanza/move\(N\) veces.
Ejemplo
Entrada
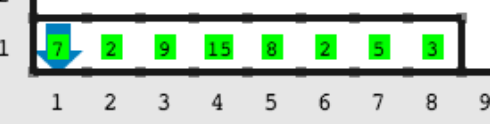
Salida
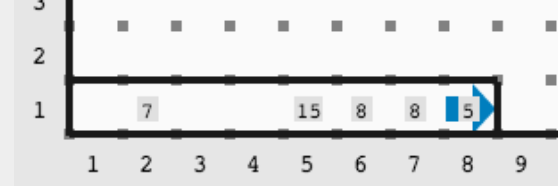

Comentarios