Descripción

Karel se enfrenta a un grupo de monstruos. La vida de cada uno está representada por un montón de zumbadores. Cada segundo, Karel puede hacer una de las siguientes dos acciones:

1. Matar un monstruo, no importa la cantidad de vida que tenga.
2. Elegir ~2~ monstruos que aun estén vivos y disminuir la vida de ambos ~X~ puntos cada uno.

Si un monstruo llega a ~0~ o menos puntos de vida muere.

Ayuda a Karel a calcular el menor número de segundos que tardará en eliminar a todos los monstruos.

En la fila del mundo de Karel habrá montones de zumbadores, sin espacios entre ellos, que representan la vida de los monstruos a los que Karel se enfrenta. En la primera columna de la fila ~2~ habrá un montón de zumbadores que representa el número ~X~, la cantidad de vida que disminuyen los monstruos cuando se usa la acción ~2~.

Problema

Escribe un programa que dado el montón que representa ~X~ y la lista con la vida de los monstruos determine el menor número de segundos que requiere Karel para matarlos a todos.

Tu programa deberá dejar en la casilla ~(1, 1)~ un montón de zumbadores igual a la cantidad mínima de turnos que se necesitan para derrotar a los monstruos.

Ejemplo

Entrada

Salida

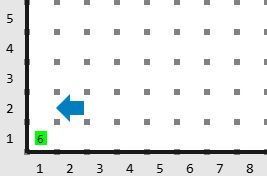
Explicación

Los valores de vida de los monstruos son: ~(6, 4, 7, 1, 3, 7, 8)~. La acción dos baja ~X = 5~ puntos de vida a cada monstruo. Karel puede hacer las siguientes acciones:

• Utilizar la acción dos en el primer y segundo monstruo. El primer monstruo quedará con una vida igual a ~1~ y el segundo morirá. Las vidas de los monstruos quedan ~(1, -, 7, 3, 7, 8)~.
• Utilizar nuevamente la acción ~2~ en el primer y tercer monstruo, las vidas quedan ~(-,-,2,1,3,7,8)~.
• Utilizar la acción ~2~ en el tercer y cuarto monstruo, las vidas quedan ~(-,-,-,-,3,7,8)~.
• Utilizar la acción ~1~ en los monstruos restantes, al cabo de ~3~ segundos más, todos los monstruos habrán sido eliminados.

En total Karel requirió de ~6~ segundos.

Consideraciones

• Karel inicia en la posición ~(1, 1)~ orientado al norte.
• Karel lleva infinitos zumbadores en la mochila. Los montones de la primera fila (vidas de los monstruos) no tienen espacios entre ellos y pueden contener entre ~1~ y ~100~ zumbadores.
• El montón de la segunda fila que representa ~X~ puede contener entre ~1~ y ~100~ zumbadores.
• El mundo de Karel es un cuadrado de ~100 x 100~ sin paredes internas.
• Para obtener los puntos, tu programa deberá dejar en la posición ~(1, 1)~ un montón igual a la cantidad mínima de segundos que Karel requiere para derrotar a todos los monstruos.

Subtareas

En este problema, los casos de cada subtarea se encuentran agrupados. Para obtener el puntaje de una subtarea deberás resolver correctamente todos los casos del grupo.

• (25 puntos): ~X = 100~
• (25 puntos): Todos los monstruos tienen la misma vida.
• (25 puntos): La vida de los monstruos nunca decrece conforme avanza la columna de su posición.
• (25 puntos): Sin restricciones adicionales.