Fernanda convenció a Karel de ir a estudiar mecatrónica con ella. Cómo Fer es influyente, le consiguió a Karel una beca del 100%. Para mantener su beca, Karel debe tener un promedio mínimo. Sin embargo, este primer semestre Karel se ha sentido triste por estar lejos de casa y sus calificaciones no fueron las que esperaba.

Karel sabe que debe mantener la beca para seguir estudiando, utilizando sus habilidades computacionales ha sido capaz de hackear la base de datos y puede borrar un número \(N\) de sus calificaciones del semestre. El número \(N\) es menor que la cantidad de materias que cursó.

Luego de conectarse a la base, Karel quedó agotado y ya no le da la cabeza para hacer las cuentas. Karel te dice el promedio mínimo que debe sacar, la cantidad \(N\) de calificaciones que puede borrar de la base y la lista de calificaciones. Ayuda a Karel a determinar si puede o no lograr el promedio que necesita.

En el mundo habrá al menos \(3\) filas:

• En la fila \(1\) a partir de la primera columna estarán las calificaciones de Karel representadas como montones de zumadores. No hay espacios entre las calificaciones.
• En la fila \(2\) habrá un montón de zumbadores que representa la cantidad \(N\) de calificaciones que Karel puede borrar de la base.
• En la fila \(3\) habrá un montón de zumbadores que representa el promedio que Karel debe tener para mantener su beca.

Ayuda a Karel a determinar si es posible, o no, lograrlo.

Problema

Escribe un programa que dadas las calificaciones, el número \(N\) que se puede borrar y el promedio requerido, determine si es posible, o no, alcanzarlo.

Karel debe apagarse orientado al norte si es posible lograr el promedio o apagarse orientado al sur si NO es posible.

Ejemplos

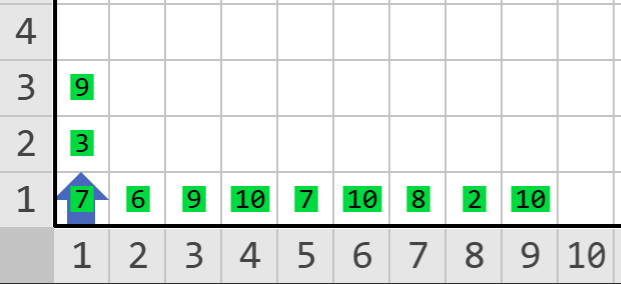
Entrada

Salida

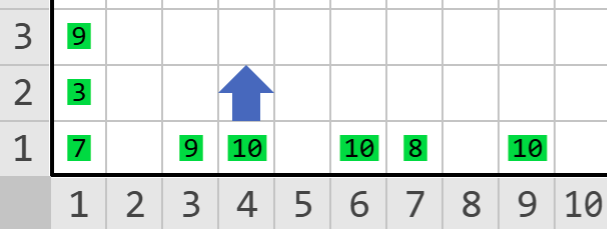
Descripción

Karel puede eliminar \(3\) calificaciones y requiere un promedio de \(9\). Al eliminar las calificaciones \(6\), \(7\) y \(2\) Karel queda con seis calificaciones \((7, 9, 10, 10, 8, 10)\) que suman \(54\) por lo que su promedio es de \(9\). Karel puede mantener la beca y por lo tanto debe apagarse orientado al norte.

Consideraciones

• Karel inicia en la posición (1, 1) orientado al norte.
• Karel lleva infinitos zumbadores en la mochila.
• El mundo de Karel es un cuadrado de \(100\) filas por \(100\) columnas.
• Los montones de la primera fila tienen valores entre \(1\) y \(100\). No hay espacios libres entre los zumbadores.
• El montón de la segunda fila representa el número \(N\) y siempre será menor a la cantidad de calificaciones. El número de calificaciones que puedes borrar puede ser \(0\).
• El montón de la tercera fila representa el promedio mínimo requerido y será un número entre \(1\) y \(100\).
• Para obtener los puntos, tu programa deberá dejar a Karel orientado al norte si es posible alcanzar el promedio y orientado al sur si NO lo es.

Subtareas

En este problema, los casos de cada subtarea se encuentran agrupados. Para obtener el puntaje de una subtarea deberás resolver correctamente todos los casos del grupo.

• (25 puntos): El promedio mínimo requerido es \(2\) y todas las calificaciones son menores o iguales a \(2\).
• (25 puntos): Puedes eliminar todas las calificaciones menos una.
• (25 puntos): El número de calificaciones que puedes borrar es \(0\).
• (25 puntos): Sin ninguna restricción.