Hay \(n\) magos en una fila numerados del 1 al n de izquierda a derecha. Cada mago tiene una capa de invisibilidad que puede llevar puesta en el lado izquierdo o en el lado derecha. Harry camina desde la posición del mago 1 hasta la posición del mago \(n\) \((1 \leq n \leq 105)\), y registra cuantos magos ve desde la posición de cada mago.

Un mago en la posición \(j\) es visible desde la posición \(i\) si:

• El mago en la posición \(j\) tiene la capa de invisibilidad a la izquierda de su traje y \(i \geq j\).
• El mago en la posición \(j\) tiene capa de invisibilidad a la derecha de su traje \(i \leq j\).

En particular nota que el mago \(i\) siempre es visible desde la posición \(i\).

La lista de Harry es muy antigua, pero después de investigar mucho lograste descifrarla. La lista es un arreglo \(a\) de \(n\) elementos, tal que \(a_i\) \((1 \leq a_i \leq n)\) es la cantidad de magos que vió desde la posición \(i\). Tu tarea es contar cuantas de todas las posibles formas en las que los magos pudieron llevar sus capas, son consistentes con la información de la lista.

Cuenta de cuantas formas distintos se pudieron haber organizado los magos. Dos arreglos de magos son distintos si existe alguna posición en la fila cuyos magos tienen orientaciones distintas de capas.

Entrada

• En la primera línea de la entreada un único entero \(t\), la cantidad de subcasos de prueba. siguen \(t\) casos de prueba, cada uno consiste de dos líneas.
• En la primera línea de cada caso de prueba, un único entero \(n\), la cantidad de magos en la fila.
• En la segunda línea \(n\) enteros separados por un espacio que indican el valor \(a_i\), la cantidad de magos visibles registrados desde la posición \(i\) en la lista de Harry.

Salida

• Para cada subcaso de prueba, imprime un único entero indicando la cantidad formas distintas en las que se pudieron haber organizado los magos.

Ejemplo

Entrada

7
1
1
4
4 4 3 2
3
1 3 2
2
2 1
3
2 2 2
3
3 2 3
3
3 2 2

Salida

2
1
0
1
2
0
0

A continuación se muestra una ilustración del segundo subcaso de prueba:

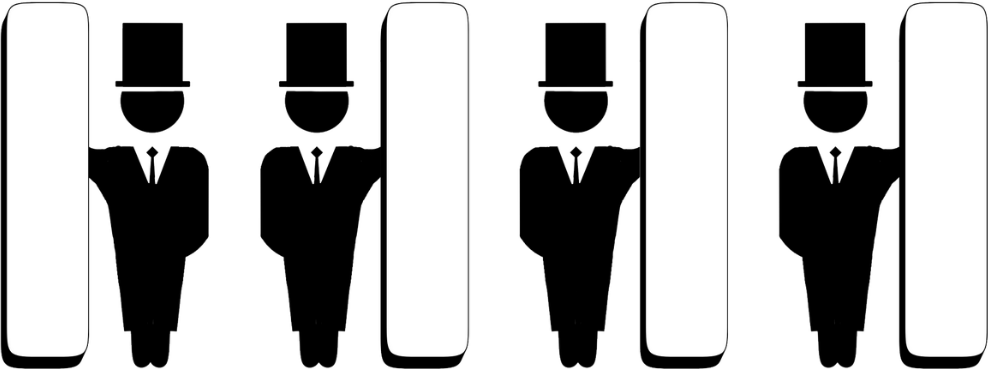
El mago \(1\) tiene la capa de invisibilidad a la izquierda, mientras que los magos \(2, 3\) y \(4\), la tienen a la derecha.

• Desde la posición \(1\), podemos ver a los magos \(1, 2, 3,\) y \(4\).
• Desde la posición \(2\), podemos ver a los magos \(1, 2, 3,\) y \(4\).
• Desde la posición \(3\), podemos ver a los magos \(1, 3,\) y \(4\).
• Desde la posición \(4\), podemos ver a los magos \(1\) y \(4\).

Por lo tanto, la lista de Harry termina siendo \(4, 4, 3, 2\). Se puede mostrar que este es el unicó arreglo de capas posible.

En el tercer caso, se puede mostrar que Harry no pudo haber obtenido su lista de ningún arreglo de capas. En el quinto caso, nota que hay dos posibles arreglos de capas a partir de los cuales Harry pudo haber obtenido la lista:

• El mago \(1\) portando la capa a la izquierda, el mago \(2\) a la derecha, y el mago \(3\) a la izquierda.
• El mago \(1\) portando la capa a la derecha, el mago \(2\) a la izquierda, y el mago \(3\) a la derecha.

Consideraciones

• \(1 \leq t \leq 104\).
• \(1 \leq n \leq 105\).
• \(1 \leq a_i \leq n\).
• Se garantiza que la suma de \(n\) sobre todos los casos no excede \(10^5\).

Subtareas

• Subtarea 1 (4 puntos): \(n = 2\).
• Subtarea 2 (12 puntos): \(a_1 = n\).
• Subtarea 3 (31 puntos): \(n \leq 12\).
• Subtarea 4 (53 puntos): Sin restricciones adicionales.