Karel es un coleccionista de poderes, cada poder es un número representado por un montón de zumbadores.

Su hermana, Gretel también colecciona poderes y quiere comparar su colección con la de Karel.

Para compararlas, Karel coloca su colección en la primera fila, mientras que Gretel coloca la suya en la segunda fila. Además de que pusieron una pared al final de las colecciones para delimitarlas. Ambas colecciones son del mismo tamaño.

Por ejemplo, si Karel tiene de colección de longitud 6 formada por los poderes: \([1, 3, 2, 0, 3, 8]\), y Gretel tiene una colección de: \([1, 2, 3, 6, 3, 9]\). Entonces el mundo se vería de la siguiente forma:

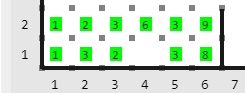
Karel y Gretel quieren saber en cuántos lugares la colección de Karel y Gretel coinciden.

La colección de Karel y Gretel coincide en el mismo lugar si tienen el mismo poder en la misma columna. Por ejemplo, la colección anterior coincide en \(2\) lugares, resaltados a continuación:

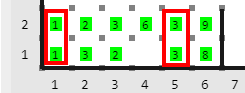
Determina en cuantos lugares las colecciones coinciden Deja la respuesta en la casilla \((1, 3)\).

Ejemplo 1

Mundo inical

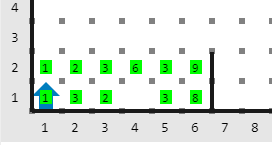
Mundo final

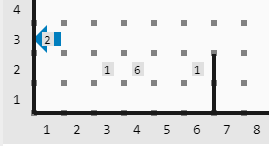
Ejemplo 2

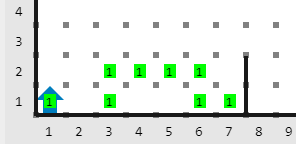
Mundo inicial

Mundo final

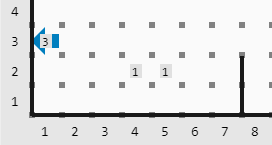
Las colecciones coinciden en el segundo, tercer y sexto poder.

Consideraciones

• Karel inicia en \((1, 1)\) orientado al Norte
• Karel tiene zumbadores infinitos
• Solo se evalúan los zumbadores en \((1, 3)\)
• La lista será de a lo mucho 99 de longitud
• El mundo mide \(100\times 100\)
• Las únicas paredes interna será la que delimita las colecciones

Subtareas

• [30 pts] La longitud de las colecciones siempre es uno.
• [30 pts] Los poderes son solo de valor 0 y valor 1, como en el segundo ejemplo.
• [40 pts] No hay consideraciones adicionales