Karel quiere repartir golosinas por el mundo, para esto, compro \(A\) golosinas picosas y \(B\) golosinas dulces.

Karel quiere separar estos golosinas en la mayor cantidad de bolsas posibles, tal que cada bolsa contenga la misma cantidad de los dos tipos de bolsa y sin dejar ningun dulce sin repartir.

Ejemplo

Si Karel tiene 10 golosinas picosas y 15 golosinas dulces, Karel puede crear 5 bolsas; cada una con 2 y 3 dulces.

Problema

Ayuda a Karel dejando la mayor cantidad de bolsas posibles en \((1, 1)\).

En \((1, 1)\) hay un montón de zumbadores \(A\), la cantidad de golosinas picosas.

En \((2, 1)\) hay un montón de zumbadores \(B\), la cantidad de golosinas dulces.

Inicial

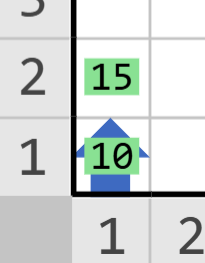
Final

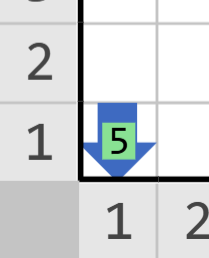
Consideraciones

• Karel inicia en \((1, 1)\) orientado al norte
• Karel tiene infinitos zumbadores en la mochila
• Solo importan los zumbadores en \((1, 1)\)
• El mundo mide 100x100 sin paredes internas ni zumbadores adicionales
• \(A\) y \(B\) valen cuanto menos 1 y a lo mucho 100.

Consideraciones

• (20 pts) La respuesta será 1 o 5
• (35 pts) El valor de alguno de los dos será 12.
• (45 pts) No hay consideraciones adicionales