Historia

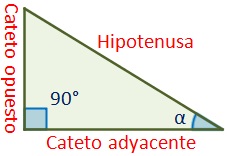
El gran Kareltágoras descubrió que para los triángulos rectángulos (estos son los triángulos que tienen un ángulo de 90°) \(a^2+b^2=c^2,\) donde \(a\) es el cateto adyacente, \(b\) es el cateto opuesto y \(c\) es la hipotenusa.

Problema

Ayuda a Kareltágoras a saber el valor de \(c^2\) y saber si \(c\) es entero. El tamaño de los lados \(a\) y \(b\) coinciden con el largo y ancho del mundo.

Ejemplos

Entrada

Salida

Explicación

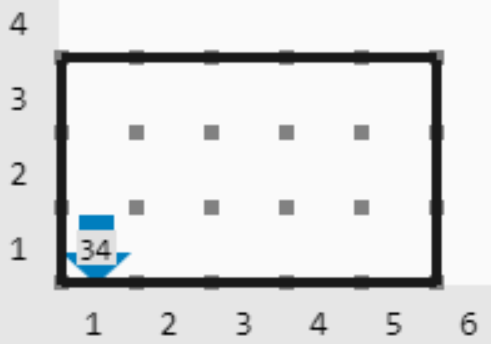
En este caso los lados del triángulo miden 3 y 5, entonces \(c^2\) es 34 y por lo tanto \(c\) no es entero.

Consideraciones

• Karel inicia en la casilla (1,1) viendo al norte.
• Karel tiene infinitos zumbadores en la mochila.
• Solo se evalúan los zumbadores de la casilla (1,1).

Subtareas

• En el 77% de los casos sólo se evalúa \(c^2\).
• En el 23% de los casos restantes también se evalúa la orientación final de Karel. Si \(c\) es entero deberás dejar a Karel orientado al norte; de lo contrario, al sur.
• Los casos de esta subtarea están agrupados.