A Karel le gusta jugar con imanes (¿a quién no?). Karel tiene imanes especiales que se pueden prender y apagar y los usará en el siguiente experimento:

Karel colocará sus imanes apagados en distintas posiciones a lo largo de una línea recta. Cuando los imanes estén colocados, los prenderá todos al mismo tiempo. Al momento de prenderse cada imán se mueve en dirección al imán que tenga más cerca (si tiene dos imanes a la misma distancia, se mueve hacia la izquierda). Cuando dos imanes chocan, se apagan y se detienen.

Eventualmente todos los imanes se irán apagando y quedarán en uno o varios grupos de imanes que chocaron entre ellos.

Karel desea saber ¿cuántos grupos de imanes quedan una vez que todos los imanes se detuvieron?.

En la primera fila del mundo, a partir de la posición (1, 1), habrá montones de zumbadores. Cada montón representa la posición de un imán. Los montones irán de forma creciente, es decir, las posiciones van ordenadas. No hay espacios vacíos entre los montones.

Karel debe dejar, en la posición (1, 1) un montón de zumbadores igual al número de grupos que se formaron durante el experimento.

Problema

Escribe un programa que dadas las posiciones en las que se colocan los imanes, deje en la posición (1, 1) un montón de zumbadores igual al número de grupos de imanes que se formaron durante el experimento.

Ejemplos

Entrada

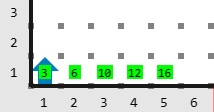
Salida

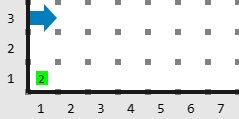
Descripción

Karel colocó 5 imanes en las posiciones 3, 6, 10, 12 y 16.

• El imán en la posición 3 se mueve hacia la derecha. Su imán más cercano es el que está en la posición 6.
• El imán en la posición 6 se mueve hacia la izquierda.
• El imán en la posición 10 se mueve hacia la derecha.
• El de la posición 12 hacia la izquierda.
• El de la posición 16 hacia la izquierda.

Eventualmente se crearán 2 grupos de imanes, uno formado por los imanes en la posición 3 y 6. Otro formado por los imanes en las posiciones 10, 12 y 16. Por lo tanto, el resultado es 2.

Consideraciones

• Karel inicia en la posición (1, 1) orientado al norte.
• Karel lleva infinitos zumbadores en la mochila.
• Sólo habrá zumbadores en la fila 1 del mundo.
• Los montones de la fila 1 pueden tener entre \(1\) y \(100\) zumbadores.
• No hay espacios vacíos entre los montones de zumbadores y estos siempre van ordenados.
• Para obtener los puntos, tu programa deberá dejar en la posición (1, 1) un montón igual a la cantidad de grupos que se forman.

Subtareas

En este problema, los casos de cada subtarea se encuentran agrupados. Para obtener el puntaje de una subtarea deberás resolver correctamente todos los casos del grupo.

• (10 puntos): Hay 3 imanes en el mundo.
• (28 puntos): Hay 4 imanes en el mundo.
• (30 puntos): Puede haber cualquier cantidad de imanes pero el número de grupos que se forman siempre será 1 ó 2.
• (32 puntos): Puede haber cualquier cantidad de imanes y quedar cualquier cantidad de grupos.