Karel gusta mucho de los juegos de cartas como Pokemón. Su juego preferido es el Karel-mon.

El Karel-mon se juega entre dos jugadores. Cada jugador tiene un mazo de cartas y cada carta tiene un número escrito. Los turnos se van alternando y se juegan de la siguiente forma. El jugador con el turno muestra una carta, si el otro jugador puede mostrar una carta con el mismo número, ambas cartas se cancelan, se descartan y continúa el juego.

Un jugador pierde si:

• Es su turno y no tiene cartas para tirar, es decir, se le acabaron las cartas.
• No tiene ninguna carta con el número que mostró el jugador en turno.

Karel está revisando antiguas partidas de campeones mundiales de karel-mon, ayúdale a determinar qué jugador podría haber asegurado el triunfo si hubiera jugado de manera óptima.

El mundo de Karel contendrá los mazos de ambos jugadores. En la primera fila hay montones de zumbadores que representan el mazo del primer jugador, cada montón representa una carta y el número de zumbadores en el montón representa el número en la carta. En la segunda fila hay montones de zumbadores que representan el mazo del segundo jugador.

Tu programa deberá dejar a Karel orientado al norte si el primer jugador puede asegurar su triunfo u orientado al sur si el que lo puede asegurar es el segundo jugador.

Problema

Escribe un programa que dados los mazos de cartas de ambos jugadores determine quién de ellos puede asegurar el triunfo y deje a Karel orientado al norte si el ganador es el primer jugador u orientado al sur si es el segundo.

Ejemplos

Entrada

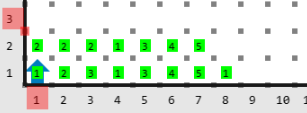
Salida

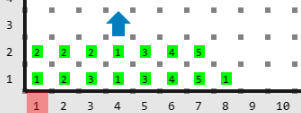
Descripción

En este problema el primer jugador puede asegurar el triunfo de la siguiente forma:

• En el primer turno el primer jugador tira una carta con el número \(1\).
• El segundo jugador puede _contestar_ y el juego continua.
• En el siguiente turno, sin importar lo que tire el segundo jugador, el primero tendrá una carta para _contestar_.
• Finalmente en el tercer turno, el primer jugador vuelve a tirar una carta con el número \(1\).
• El segundo jugador ya no tiene más cartas con el número \(1\) por lo que pierde el juego.

Karel queda orientado hacia el norte porque el primer jugador puede asegurar el triunfo.

Consideraciones

• Karel inicia en la posición (1, 1) orientado al norte.
• Karel lleva infinitos zumbadores en la mochila.
• El mundo de Karel es de tamaño \(100 \times 100\).
• Sólo habrá zumbadores en las filas 1 y 2 del mundo.
• Los montones pueden tener entre \(1\) y \(100\) zumbadores.
• No hay espacios vacíos entre los montones de zumbadores.
• Para obtener los puntos, tu programa deberá dejar a Karel en la orientación correcta. No importa la posición final de Karel ni los zumbadores que queden en el mundo.

Subtareas

En este problema, los casos de cada subtarea se encuentran agrupados. Para obtener el puntaje de una subtarea deberás resolver correctamente todos los casos del grupo.

• (7 puntos): El primer jugador sólo tiene \(1\) carta en su mazo.
• (17 puntos): Ambos jugadores tienen 2 cartas en su mazo.
• (12 puntos): Los mazos de ambos jugadores tienen exactamente las mismas cartas aunque pueden estar en orden distinto.
• (22 puntos): Ninguno de los mazos tiene cartas repetidas, es decir, en cada mazo, cada número aparece únicamente una vez.
• (42 puntos): Sin restricciones adicionales.