En la ciudad de Karelópolis se llevan a cabo juegos de _combate territorial_. En dichos juegos, dos pelotones de karels adolescentes, cada uno con un color asignado, tratan de pintar la mayor cantidad de piso de un mundo rectangular usando pistolas de agua.

Cada color se representa con un número distinto. Si un karel dispara sobre una posición, la pinta del color de su pelotón. Si jugadores de ambos pelotones disparan sobre la misma posición la pintura se mezcla y el color que queda se representa con la suma de los números de los colores de ambos pelotones.

Al final del juego se cuentan la cantidad de posiciones de cada color, las posiciones con color mezclado no cuentan para ningún pelotón. El pelotón que haya pintado más posiciones se considera el ganador.

El mundo de karel representa el final de una partida. El mundo es un rectángulo sin paredes internas y con montones de zumbadores. La cantidad de zumbadores en cada montón representa el color del que quedó pintada esa posición. Si no hay zumbadores en una posición significa que ningún pelotón intentó pintarla.

Dado un mapa al final de una partida, coloca en la esquina \((1, 1)\) del mundo el color del pelotón ganador.

Se asegura que siempre hay un pelotón ganador. Es decir, no hay empates.

Problema

Dado el mapa del final de una partida, escribe un programa que determine el pelotón ganador y deje en la posición \((1, 1)\) un montón de zumbadores con el color asignado al pelotón que ganó el _combate_.

Ejemplos

Entrada

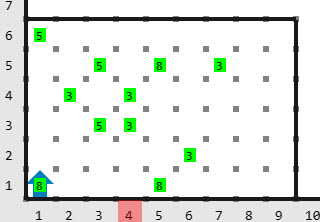
Salida

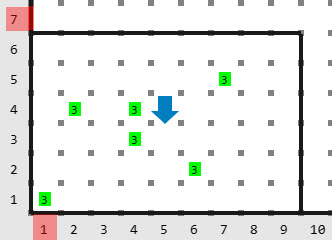
Descripción

Los colores asignados a los pelotones son el \(3\) y el \(5\). En el mundo hay cinco posiciones pintadas con el color \(3\), tres posiciones pintadas con el color \(5\) y tres posiciones en las que ambos pelotones pintaron.

Por lo tanto el ganador fue el pelotón con el color \(3\) y tu programa debe dejar en la posición \((1, 1)\) el número \(3\).

Consideraciones

• Karel inicia en la posición \((1, 1)\) orientado al norte.
• Karel lleva inifinitos zumbadores en la mochila.
• El mundo de Karel es un rectángulo sin paredes internas.
• Los montones de zumbadores pueden estar en cualquier lugar del mundo, pero sólo habrá montones con tres valores distintos, el pelotón 1, el pelotón 2 y las posiciones pintadas por ambos.

Subtareas

En este problema, los casos de cada subtarea se encuentran agrupados. Para obtener el puntaje de una subtarea deberás resolver correctamente todos los casos del grupo.

• (10 puntos): Sólo un pelotón pintó posiciones del mundo.
• (22 puntos): No hay ninguna posición en la que hayan pintado ambos pelotones. Además, el ancho del mundo es mayor que cualquiera de los colores asignados a los pelotones.
• (24 puntos): El ancho del mundo es mayor que la suma de los colores asignados a ambos pelotones.
• (21 puntos): No hay posiciones pintadas por ambos pelotones. El ancho y alto del mundo son menores que los colores asignados a los pelotones.
• (23 puntos): El alto y ancho del mundo son menores que los colores asignados a los pelotones.