Karel está encargado de actualizar la red de antenas de una compañía de telefonos celulares. La compañía cuenta actualmente con algunas antenas ya colocadas. La tarea de Karel es revisar si existe comunicación entre todas las parejas de antentas y en caso de que no sea así, le diga a la compañía ¿cuántas antenas deben agregar para logarlo?

Dos antenas puede comunicarse entre sí si están la misma fila o la misma columna. De igual forma dos antenas \(A\) y \(B\) puede comunicarse entre sí si existe un conjunto de antenas \(C = c_1, c_2, \ldots, c_m\) tal que \(A\) comparte fila o columna con \(c1\), \(c1\) comparte fila o columna con \(c_2\) y así sucesibamente hasta que \(c_m\) comparte fila o columna con \(B\).

Las antenas se representan en el mundo de Karel como montones de \(1\) zumbador.

En caso de que haya parejas de antenas que no están comunicadas, la compañía puede agregar nuevas antenas en cualquier parte del mundo. Sin embargo, como cualquier infraestructura, agregar antenas cuesta, por lo que han pedido la ayuda de Karel para saber cuál es el costo mínimo que requieren invertir.

Problema

Escribe un programa que dadas las antenas de la compañía determine cuál es el mínimo número de antenas que se deben agregar a la red para asegurar que todas las parejas de antenas puedan conectarse.

Karel deberá dejar en la esquina \((1, 1)\) del mundo un montón de zumbadores igual a la cantidad mínima de antenas nuevas que se requieren.

Ejemplos

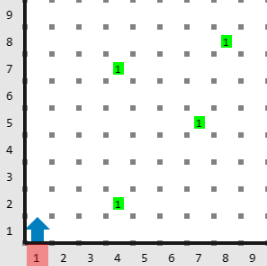
Entrada

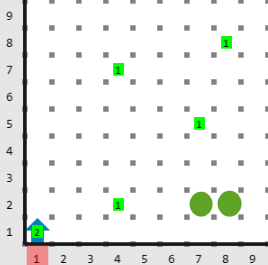
Salida

Descripción

En el mundo hay cuatro antenas. Las antenas en la fila \(4\) pueden comunicarse entre ellas por compartir columna, sin embargo no pueden comunicarse con ninguna de las antenas en las columnas \(7\) u \(8\).

Hay muchas formas de colocar nuevas antentas que permitan la comunicación. Una opción es colocar dos nuevas antenas en la fila \(2\) y columnas \(7\) y \(8\) en las posiciones mostradas con un círculo verde en la figura. Estas nuevas antentas permitirían la comunicación entre cualquier pareja de antenas en el mundo.

Independientemente de las posiciones que escojas para las nuevas antentas, el mínimo número que requieres es dos antentas. Por lo tanto, Karel debe dejar un montón de \(2\) zumbadores en la posición \((1, 1)\)

Consideraciones

• Karel inicia en la posición (1, 1) orientado al norte.
• Karel lleva infinitos zumbadores en la mochila.
• En el mundo sólo hay montones de \(1\) zumbador que representan las antentas.
• En el mundo habrá al menos una antena.
• El mundo de Karel es un rectángulo sin paredes internas.
• Para obtener los puntos, tu programa deberá dejar en la posición (1, 1) un montón igual a la cantidad mínima de antenas nuevas que se requieren para comunicar toda la red.

Subtareas

En este problema, los casos de cada subtarea se encuentran agrupados. Para obtener el puntaje de una subtarea deberás resolver correctamente todos los casos del grupo.

• (25 puntos): En el mundo hay únicamente 2 antenas.
• (25 puntos): El mundo tiene dos columnas de ancho.
• (25 puntos): Todas las antenas están únicamente en dos columnas distintas.
• (25 puntos): Sin ninguna restricción.