Darel está aprendiendo ajedrez, aun no sabe mucho, pero le gusta mucho jugarlo. Una de las cosas que más le llama la atención a Darel es el patrón de casillas blancas y negras que tiene el tablero.

Como su mentor, Karel piensa muchos ejercicios creativos para ayudar a Darel a mejorar, el día de hoy están trabajando con el siguiente. Karel toma una hoja cuadriculada, dibuja un rectángulo y rellena algunos de sus cuadros (posiblmente cero) de color negro. Darel debe ver la hoja y determinar si el resto del rectángulo puede dibujarse con un patrón de tablero de ajedrez.

Aunque el ejercicio fue interesante al inicio, después de un rato Darel se aburrió y te pidió tu ayuda para poder resolver los ejercicios.

El mundo de Karel representa la hoja del ejercicio. Las paredes que rodean el mundo son las que delimitan el rectángulo. Las casillas con montones de \(1\) zumbador representan los cuadros que Karel dibujó en negro.

Problema

Escribe un programa que dado el mundo que representa el ejercicio determine si es posible llenar el rectángulo con un patrón tipo ajedrez o no. En caso de que sea posible, Karel debe apagarse viendo al norte. Si no es posible Karel debe apagarse viendo al sur.

Ejemplos

Entrada

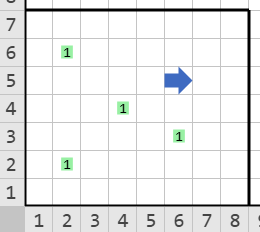
Salida

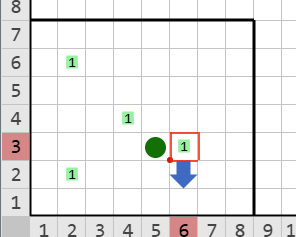
Descripción

En este caso el mundo no puede llenarse con un patrón de ajedrez ya que la posición marcada con un círculo verde debe ir dibujada en color negro sin embargo, esto haría que quede junto de la casilla en el cuadro rojo la cual ya está dibujada de negro. Por lo tanto Karel se apaga viendo al sur.

Consideraciones

• Karel inicia dentro del rectángulo con posición y orientación desconocida.
• Karel NO lleva zumbadores.
• Todos los montones son de \(1\) zumbador y representan las casillas pintadas de negro.
• El mundo es un rectángulo sin paredes internas que puede medir hasta \(100\) por \(100\).
• Para obtener los puntos, Karel debe apagarse viendo al norte si el tablero puede rellenarse con un patrón de ajedrez o viendo al sur en caso contrario.

Subtareas

En este problema, los casos de cada subtarea se encuentran agrupados. Para obtener el puntaje de una subtarea deberás resolver correctamente todos los casos del grupo.

• (25 puntos): El rectángulo tiene alto de \(1\) fila o ancho de \(1\) columna.
• (25 puntos): Hay exactamente dos casillas pintadas en el rectángulo (dos posiciones con \(1\) zumbador).
• (25 puntos): Hay un zumbador en la casilla \((1, 1)\).
• (25 puntos): Sin restricciones adicionales.