No todos lo saben, pero los Karels tienen muchas vidas, algunos dicen que 9, otros creen que más.

El famoso aventurero Karel con botas perdió una de sus vidas hoy :(, por suerte, todavía le sobran algunas. Le preocupa que no sabe exactamente cuántas le quedan y ha pedido tu ayuda para saberlo.

Cuando Karel con botas inicia una nueva vida, lo hace con su energía al máximo. Cada año su energía disminuye en \(1\). Esa vida termina si su energía llega a \(0\) o algún evento inesperado (accidente, batalla, enfermedad, etc) la interrumpe. En cualquiera de los casos, al terminar una vida inicia una nueva con su energía de nuevo al máximo.

En el instante en que perdió su vida hoy, los años de todas sus vidas pasaron frente a sus ojos. Lo malo es que los años pasaron en desorden y Karel no sabe cuándo empezó y terminó cada vida, por lo que no pudo contar cuántas llevaba.

En la fila 1 del mundo de Karel hay montones de zumbadores que representan la _energía_ que tenía Karel en cada uno de los años que vio. Aunque están en desorden, Karel vio todos sus años de vida. Recuerda que cada que inicia una vida, Karel tiene la _energía_ al máximo.

Problema

Escribe un programa que le diga a Karel cuántas vidas ha vivido hasta este momento. Tu programa debe dejar un montón de zumbadores en la posición \((1, 1)\) indicando la cantidad de vidas que Karel ha vivido.

Ejemplos

Entrada

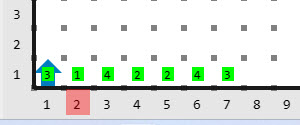
Salida

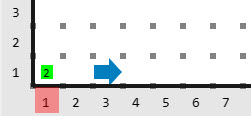
Descripción

Karel ha vivido ya vivido dos vidas, una de ellas terminó cuando su energía era \(2\) y la otra llegó hasta el final.

Consideraciones

• Karel inicia en la posición \((1, 1)\) orientado al norte.
• Karel lleva infinitos zumbadores en la mochila.
• El mundo de Karel es un rectángulo sin paredes internas.
• Los montones que representan la energía en los años que ha vivido Karel se encuentran en la fila 1.
• No existen espacios vacíos entre los montones de la fila \(1\).
• Para obtener los puntos tu programa deberá dejar un montón con la cantidad de vidas que Karel ha vivido en la posición \((1, 1)\).

Subtareas

En este problema, los casos de cada subtarea se encuentran agrupados. Para obtener el puntaje de una subtarea deberás resolver correctamente todos los casos del grupo.

• (10 puntos): La energía máxima de Karel es igual a \(1\).
• (16 puntos): Los años de vida de Karel pasan en orden.
• (14 puntos): La energía máxima de Karel es igual a \(10\).
• (20 puntos): El alto del mundo es mayor que la energía máxima de Karel.
• (22 puntos): El alto del mundo de Karel es \(1\).
• (18 puntos): Karel puede ejecutar la instrucción avanza/move un máximo de \(2N\) veces donde \(N\) es el ancho del mundo.