Karel coludido en el terrible mundo de la política y las obras públicas

Karel está construyendo casas, pero como le dieron las obras por nepotismo y soborno, y no por conocimiento, las está haciendo muy mal. Literal hizo dos rectángulos que además se intersectan.

De forma muy aleatoria y sin ninguna explicación puso las bases de cada casa regadas por doquier, de modo que cuando termine de poner todo el cemento se encontrará con que las dos casas se intersectarán. A pesar de la mediocridad del proyecto, a los gobernantes les pareció demasiado y quieren saber cómo quedará la intersección.

El área de la primera casa se define como el rectángulo más pequeño que contenga todos los montones de 1 zumbador.

El área de la segunda casa se define como el rectángulo más pequeño que contenga todos los montones de 2 zumbadores.

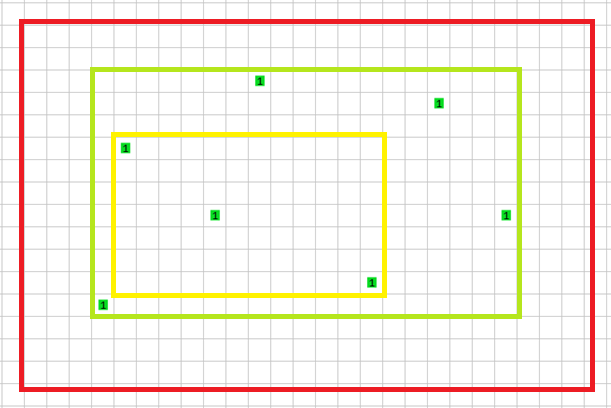
En la imagen podemos observar que a pesar de que el rectángulo amarillo sea el más pequeño, esta no es el área ya que dentro de no están todos los zumbadores. El rectángulo rojo contiene todos los zumbadores pero no es el más pequeño. La respuesta es el rectángulo verde.

La intersección de ambas casas se define como el rectángulo en el que tanto la primera y segunda casa existen.

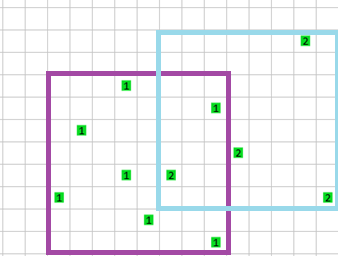
En este caso el rectángulo morado es el área de la primera casa, y el rectángulo azul de la segunda.

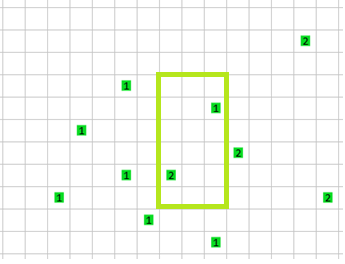
Por lo tango el rectángulo verde es la intersección de las áreas.

Problema

Dados montones de 1 y 2 zumbadores, dibuja la interesección con montones de 3 zumbadores.

Ejemplo

*** l

Consideraciones

• Karel inicia en la casilla 1x1 mirando hacia el Norte.
• El mundo es de 30x30.
• No importa la orientación ni posición final de Karel. Solo los montones de 3 zumbadores.
• La cantidad de zumbadores de cada montón será 1 o 2.
• Por cada rectángulo habrá al menos dos montones de zumbadores.

Subtareas

• Subtarea 1 (25 puntos): Las áreas y la intersección tendrán esta forma: 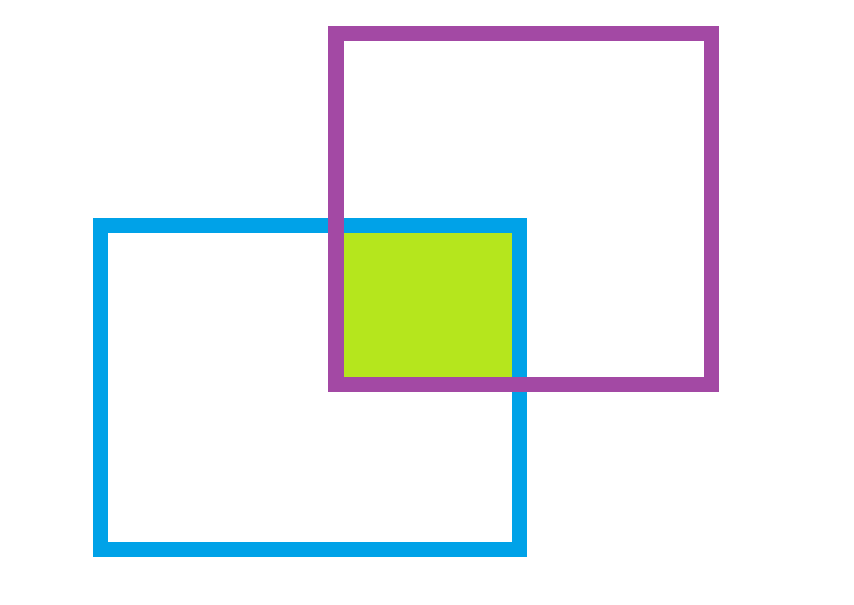El primer rectángulo será siempre el azul.
• Subtarea 2 (25 puntos): La altura del segundo rectángulo será de 1.
• Subtarea 3 (25 puntos): Habrá en total 4 montones de zumbadores, dos por cada rectángulo.
• Subtarea 4 (25 puntos): Sin consideraciones adicionales.