La tubería más larga

Karel consiguió un trabajo de verano en una planta industrial. Entre sus responsabilidades está supervisar una red de tuberías que transportan material peligroso.

La red de tuberías se representa como pasillos delimitados por paredes de ancho uno. Las tuberías pueden bifurcarse, pero nunca forman ciclos. La siguiente imagen muestra ejemplos de redes de tuberías válidas e inválidas:

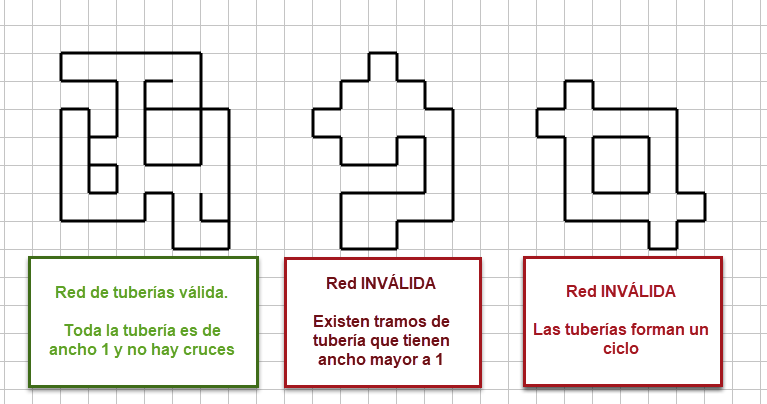
Cada casilla del mundo es una sección de tubería. Se considera que el largo de una tubería es la cantidad de secciones que contiene. Por ejemplo:

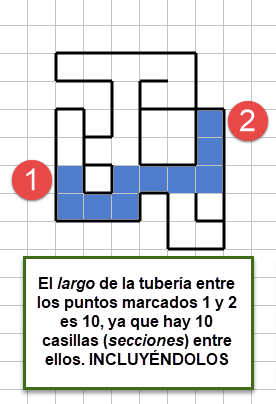
Dado que el material que se transporta es peligroso, mientras más larga sea la tubería mayor es el riesgo de un accidente.

Ayuda a Karel a determinar el largo máximo que existe entre dos secciones cualquiera de la tubería. Es decir, encuentra el largo entre las dos secciones más alejadas de la tubería.

Problema

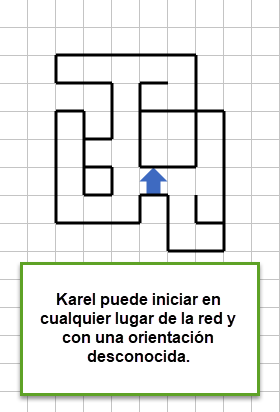
El mundo de Karel contiene paredes que representan una red de tuberías válida. Karel se encuentra en algún lugar dentro de la red de tuberías con orientación desconocida.

Tu programa debe calcular cuál es el largo máximo entre cualesquiera dos secciones de la red de tuberías.

Tu programa deberá dejar, en la posición final de Karel, un montón de zumbadores igual al largo máximo en la red de tuberías.

Entrada

Salida

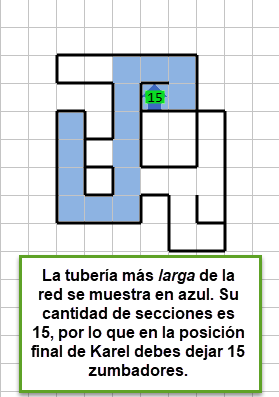
Consideraciones

• Karel inicia dentro de la red con orientación desconocida.
• Karel lleva INFINITOS zumbadores en la mochila$.
• No hay zumbadores dentro de la red de tuberías.
• No es posible salir de la red de tuberías, está totalmente delimitada por paredes.
• Las tuberías siempres son pasillos de ancho 1 con bifurcaciones, pero se asegura que no existe ningún ciclo dentro de la red.
• No importan los zumbadores que dejes en el mundo, sólo los que queden en la posición final de Karel.
• Para obtener los puntos, tu programa deberá dejar, en la posición final de Karel, un montón de zumbadores igual al largo máximo entre cualesquiera dos secciones de la red.

Subtareas

En este problema, los casos de cada subtarea se encuentran agrupados. Para obtener el puntaje de una subtarea deberás resolver correctamente todos los casos del grupo.

• ⭐ Subtarea 1 (25 puntos): La red consta de 1 único pasillo. No hay bifurcaciones.
• Subtarea 2 (25 puntos): Karel inicia en una sección que es uno de los extremos de la tubería más larga.
• Subtarea 3 (25 puntos): Karel inicia en una sección que forma parte de la tubería más larga, pero no necesariamente es el extremo.
• Subtarea 4 (25 puntos): Karel inicia en cualquier lugar de la red.