Guachimontones

Karel está visitando las zonas arqueológicas en Jalisco; los Guachimontones (unas pirámides llenas de oro).

Existe una tradición en esta zona que consiste en comenzar en la punta de la pirámide e ir bajando y sumando el oro por cada casilla por la que pases.

Tienes 3 opciones para continuar tu recorrido.

1. Abajo.
2. Diagonal izquierda.

3. Diagonal derecha.

   

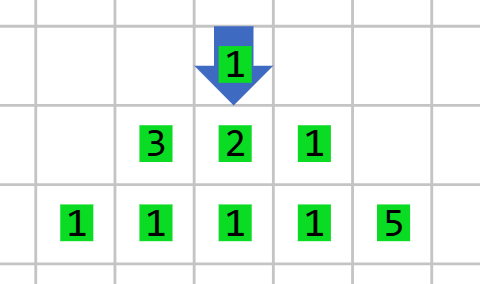
Para cada casilla quieres saber el oro acumulado máximo si comienzas en la cima de la pirámide y terminas en esa misma casilla.

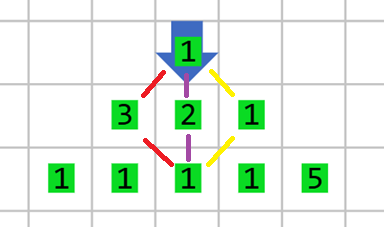
En el ejemplo, hay 3 maneras para llegar a la casilla señalada, en el camino color rojo el oro acumulado es 1 + 3 + 1 = 5, en el morado es 1 + 2 + 1 = 4, y en amarillo 1 + 1 + 1 = 3. Así que el mayor oro es 5. Si aplicamos el mismo procedimiento en cada casilla nuestra salida se verá así:

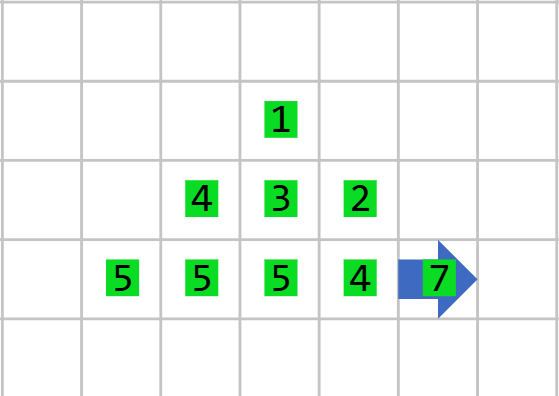
Problema

Dada una pirámide con montones de zumbadores, para cada posición dados todos los posbibles caminos posibles para llegar, deja la que maximice la suma de los zumbadores por los que pasa.

Ejemplo

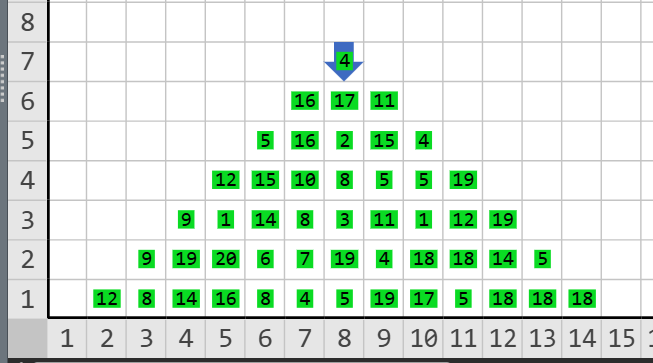
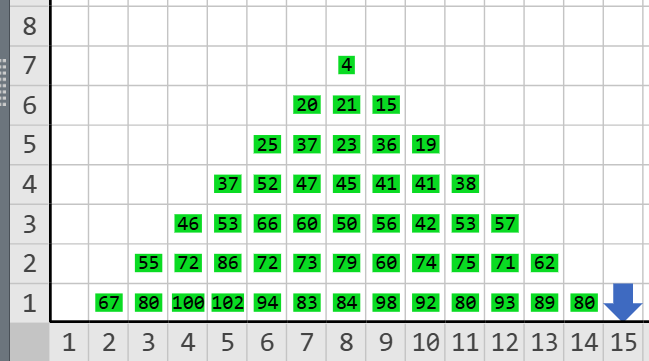
Consideraciones

• Karel inicia en la punta de la pirámide mirando hacia el Sur con infinitos zumbadores en la mochila.
• El mundo es de 100 de ancho y 100 de alto.
• No importa la orientación ni posición final de Karel. Solo los zumbadores del mundo.
• La cantidad de zumbadores de cada montón estará entre 1 y 9999.
• La fila de hasta abajo de la pirámide estará en la fila 1 del mundo.
• La primera columna de la pirámide estará en la columna 2 del mundo.
• La altura de la pirámide estará entre 1 y 49.

Subtareas

• Subtarea 1 (10 puntos): Todos los montones de zumbadores tienen exactamente un zumbador.
• Subtarea 3 (15 puntos): Todos excepto uno de los montones de zumbadores tendrán exactamente un zumbador, a exepción de uno que tendrá 2 o más zumbadores.
• Subtarea 2 (25 puntos): La altura de la pirámide es menor igual a 7.
• Subtarea 4 (50 puntos): Sin consideraciones adicionales.