Kapsule Korp ha traído una nueva tecnología a Karelópolis: cápsulas de zumbadores que se expanden. Este gran descubrimiento expande un montón de \(X\) zumbadores en un cuadrado que se extiende \(X\) casillas en las 4 direcciones desde la casilla original del montón. Cada casilla del cuadrado expandido solo tiene 1 zumbador.

Problema

Ayuda a Karel a expandir todos los montones de zumbadores que se encuentran por el mundo. Si dos o mas cuadrados expandidos se empalman debes dejar su interesección en blanco.

Ejemplos

Ejemplo 1

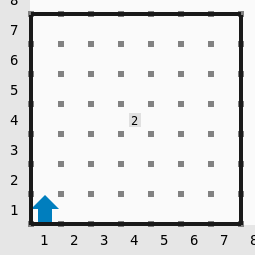
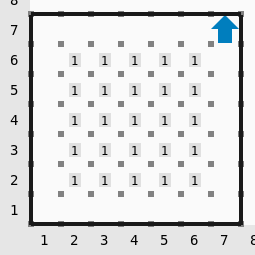
Hay un montón de \(2\) zumbadores en la casilla \((4, 4)\). El montón se expande para hacer un cuadrado de zumbadores desde la casilla \((2, 2)\) hasta la casilla \((6, 6)\)

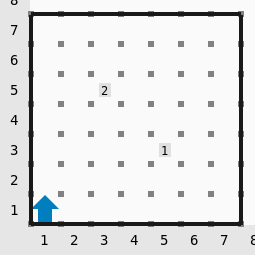
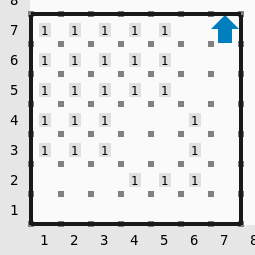
Ejemplo 2

Ejemplo de caso con intersección entre 2 cápsulas.

Consideraciones

• Karel inicia en la casilla \((1, 1)\) viendo al norte.
• Karel tiene infinitos zumbadores en la mochila.
• El mundo es rectangular sin paredes internas.
• No importa la posición ni orientación final de Karel.
• Ninguna cápsula se sale del mundo al expandirse.

Subtareas

• En el 23% de los casos las cápsulas nunca se van a intersectar al expandirse.
• En el 77% de los casos no hay consideraciones adicionales.

OMIPS 2020 (Alexis Cervantes)