Viendo las olimpiadas de Tokio te diste cuenta de que las competencias son muy cerradas, las diferencias entre competidores son de centésimas o a veces milésimas de segundo. Te preguntas ¿cuántas veces en el pasado la precisión de los relojes habrá influido en el resultado?

Por suerte Karel puede viajar al pasado, no te ha dicho como, a las antiguas olimpiadas griegas de hace más de 2,700 años. En su viaje, Karel usó un reloj atómico para medir los tiempos de los diferentes atletas con increíble precisión y regresó a nuestro tiempo con una lista de dichos valores.

Los tiempos que midió Karel se representan como una lista de montones de zumbadores en la primera fila del mundo, el número de zumbadores en el montón representa el tiempo.

Estas interesado en saber cuántos empates hubiera habido usando relojes menos precisos que el que usó Karel.

En específico, supón que un reloj tiene un _error de precisión_ \(K\) comparado con el de Karel, eso significa que para cualquier pareja de tiempos cuya diferencia sea menor o igual que \(K\), los habría considerado un empate. Por ejemplo si el reloj tiene \(K = 3\) entonces consideraría empatados tiempos de \(14\) y \(17\) ya que la diferencia entre ellos es menor o igual que \(3\).

Si todos los corredores de antaño hubieran competido por parejas, es decir, si tomas todas las parejas posibles de la lista de tiempos que trajo Karel. Cuenta ¿cuántos empates habría habido para una cierta \(K\)?

El _error de precisión_ \(K\) estará representado por un montón de zumbadores en primera columna de la segunda fila.

Problema

Escribe un programa que permita a Karel contar cuántas parejas de valores hay que estén _empatadas_ dado un _error de precisión_ \(K\) y deje un montón de zumbadores con ese número en la casilla (1, 1)

Ejemplo

Entrada 1

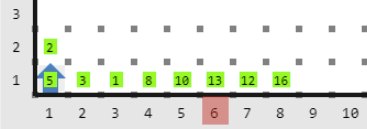
Salida 1

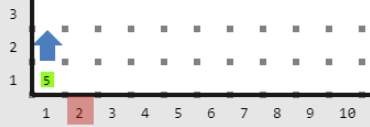
Las parejas que se consideran empate son: \([1, 3], [3, 5], [8, 10], [10, 12]\) y \([12, 13]\)

Entrada 2

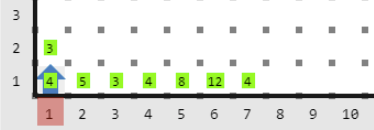
Salida 2

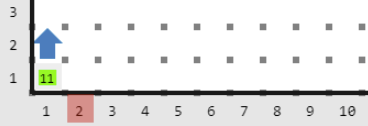
Observa que hay tres números \(4\), para diferenciarlos los llamaremos \(4_1, 4_2\) y \(4_3\). Las parejas que se consideran empate son: \([3, 4_1], [3, 4_2], [3, 4_3], [3, 5], [4_1, 4_2], [4_1, 4_3], [4_2, 4_3], [4_1, 5], [4_2, 5], [4_3, 5]\) y \([5, 8]\)

Consideraciones

• Karel inicia en la casilla (1, 1) orientado al norte.
• Karel tiene infinitos zumbadores en la mochila.
• El mundo de Karel será de \(100\) por \(100\).
• Los tiempos medidos por Karel están representados como montones en la primera fila. Los tiempos están entre \(1\) y \(99\).
• No hay espacios vacíos entre los montones que representan los tiempos.
• El _error de precisión_ \(K\) está representado por un montón en la primera columna de la segunda fila. \(K\) puede valer desde \(0\) hasta \(99\).
• Para la evaluación, sólo importa el montón de zumbadores que tu programa deje en la casilla (1, 1).

Subtareas

• (15 puntos): \(K = 0\)
• (15 puntos): \(K = 1\) y en la lista de tiempos de Karel no hay valores repetidos.
• (20 puntos): \(K = 1\) y en la lista de tiempos de Karel hay valores repetidos.
• (24 puntos): En la lista de tiempos de Karel no hay valores repetidos.
• (26 puntos): Sin restricciones adicionales