Karel se ha vuelto fanático de los viejos juegos de _Arcade_. Dichos juegos son muy simples, tanto en gráficos como en controles. Actualmente Karel está jugando un juego llamado _Derrumbe_.

En _Derrumbe_, el jugador debe obtener una _moneda_ mientras se mueve para esquivar piedras que caen por la pantalla. Derrumbe se juega por _turnos_, cada _turno_ tiene los siguientes pasos:

• El jugador decide moverse una casilla a la izquierda, una casilla a la derecha o quedarse dónde está. El jugador no puede moverse a un lugar fuera del mundo.
• Todas las piedras y la _moneda_ caen una casilla hacia abajo.
• Si cae una piedra sobre el jugador, este pierde su vida y el juego termina.
• Las piedras que llegaron hasta la fila inferior desaparecen y termina el turno.

Si al finalizar el turno, el jugador está en la misma casilla que la moneda, el jugador gana. Si la moneda llega a la fila inferior y el jugador no está en esa casilla, la moneda desaparece y el jugador pierde.

La siguiente figura muestra el desarrollo de un turno:

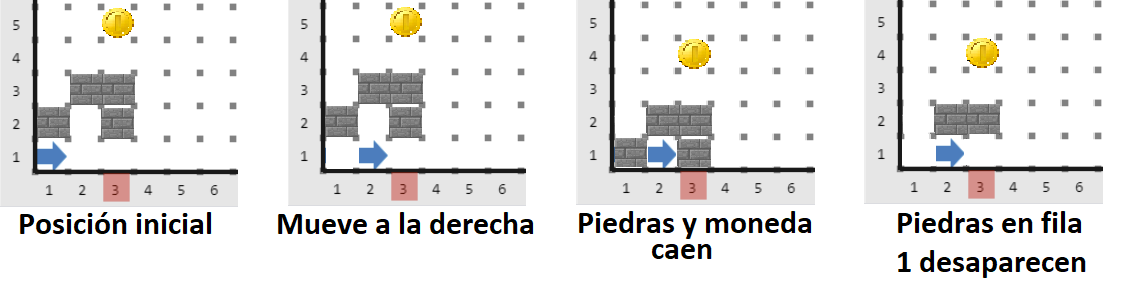
En este ejemplo, el jugador podría ganar el juego realizando los siguientes movimientos:

• Turno 1: Moverse a la derecha (este), como muestra la figura.
• Turno 2: Moverse a la izquierda (oeste).
• Turno 3: Moverse a la derecha.
• Turno 4: Moverse a la derecha y tomar la moneda.

Karel desea que le ayudes a saber si podrá ganar el juego.

El mundo de Karel representa un juego de _Derrumbe_. Karel representa al jugador y empieza en la casilla \((1, 1)\). Las piedras se representan por montones de \(1\) zumbador y la moneda se representa por un montón de \(2\) zumbadores.

Problema

Escribe un programa que permita a Karel saber si es posible ganar el juego.

• Si Karel puede ganar el juego (llegar a la moneda sin ser aplastado) deberá apagarse viendo al norte.
• Si Karel no puede ganar el juego deberá apagarse viendo al sur.

Ejemplo 1

Este es el mundo representado en la figura. En este mundo el jugador puede alcanzar la moneda, por lo que Karel debe apagarse orientado al norte.

Ejemplo 2

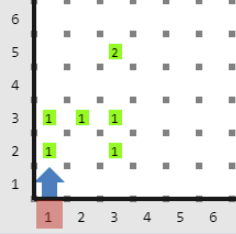
En este mundo aunque el jugador puede moverse a la derecha en el primer turno, en el segundo turno no puede evitar ser aplastado por las piedras, por lo que no alcanza la moneda y debe terminar orientado al sur.

Consideraciones

• Karel inicia en la casilla (1, 1) orientado al norte.
• Karel tiene infinitos zumbadores en la mochila.
• Sólo habra \(1\) moneda en el mundo.
• Para la evaluación, sólo importa la orientación de Karel.

Evaluación

• (23 puntos): El mundo no tendrá _piedras_, el único montón de zumbadores es el que representa la moneda.
• (29 puntos): La fila en la que está la moneda es igual a su columna, es decir la moneda se encuentra en la casilla \((x, x)\).
• (21 puntos): El tamaño del mundo será menor a \(8\) por \(8\).
• (27 puntos): Sin restricciones adicionales.